Convolutional Neural Networks (CNN)
Exploring Convolutional Neural Networks with MNIST Dataset
Program outputBuild and Train a Convolutional Neural Network (CNN) and Explore Different Layers
Table of Contents
- Aim
- Prerequisite
- Steps
- Step 1: Load the MNIST dataset into your notebook
- Step 2: Pre-processing and prepare the data for giving to the CNN
- Step 3: Building the convolutional network model
- Step 4: Vary the number of layers and repeat step 3
- Step 5: Implement the architecture of LeNet 5
- Step 6: Finally note which network gives you the best performance
Aim
To build and train a Convolutional Neural Network (CNN) on the MNIST dataset and explore the application of different layers.
Prerequisite
- Python Programming
- TensorFlow/Keras
- Convolutional Neural Networks (CNNs)
- MNIST dataset
Steps
Step 1: Load the MNIST dataset into your notebook
Load the MNIST dataset to begin the data processing and modeling steps.
Step 2: Pre-processing and prepare the data for giving to the CNN
Step 2a: Encoding the classes using one hot encoder
Convert the class labels into a binary matrix representation using one hot encoding.
Step 2b: Normalize the features
Normalize the pixel values of the images to a range between 0 and 1.
Step 3: Building the convolutional network model
Step 3a: You may choose the layers
Select and add layers to the CNN model as per requirement, including convolutional layers, pooling layers, and dense layers.
Step 3b: Print the summary and note the number of neurons and parameters of the model
Display the summary of the CNN model architecture and note the number of neurons and parameters for each layer.
Step 3c: Compile the model and train it using the training data
Compile the CNN model with appropriate loss function, optimizer, and metrics. Train the model using the training dataset, and include validation data for evaluation during training.
Step 4: Vary the number of layers and repeat step 3
Experiment by adding or removing layers from the CNN model architecture and observe the impact on model performance.
Step 5: Implement the architecture of LeNet 5
Implement the specific architecture of LeNet 5, a classic CNN architecture designed for handwritten digit recognition.
Step 6: Finally note which network gives you the best performance
Compare the performance of different CNN architectures (varying layers and LeNet 5) based on metrics such as accuracy and loss to determine which network performs the best for the MNIST dataset.
# import libraries
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from keras import Sequential
from keras.layers import Conv2D, Flatten, Input, MaxPooling2D, Flatten, AveragePooling2D, Dense
from keras.models import Model
from sklearn.preprocessing import OneHotEncoder
Task 1: Load the MNIST dataset into your notebook
# loading a dataset
mnist = tf.keras.datasets.mnist
(X_train,y_train),(X_test,y_test) = mnist.load_data()
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz
11490434/11490434 [==============================] - 0s 0us/step
X_train.shape
(60000, 28, 28)
y_train.shape
(60000,)
X_test.shape
(10000, 28, 28)
y_test.shape
(10000,)
Task 2: Pre-processing and prepare the data for giving to the CNN.
a. Encoding the classes using one hot encoder.
b. Normalize the features.
# normalizing
X_train = X_train / 255.0
X_test = X_test / 255.0
ohe = OneHotEncoder(sparse = False)
y_train = ohe.fit_transform(y_train.reshape(-1,1))
y_test = ohe.fit_transform(y_test.reshape(-1,1))
/usr/local/lib/python3.10/dist-packages/sklearn/preprocessing/_encoders.py:868: FutureWarning: `sparse` was renamed to `sparse_output` in version 1.2 and will be removed in 1.4. `sparse_output` is ignored unless you leave `sparse` to its default value.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/preprocessing/_encoders.py:868: FutureWarning: `sparse` was renamed to `sparse_output` in version 1.2 and will be removed in 1.4. `sparse_output` is ignored unless you leave `sparse` to its default value.
warnings.warn(
# Reshaping the dataset
# Building the input vector into 4D tensor (i.e 1) ([0] means keeping the first dimension as it is)
X_train = X_train.reshape(X_train.shape[0], 28, 28, 1)
X_test = X_test.reshape(X_test.shape[0], 28, 28, 1)
X_train[0].shape
(28, 28, 1)
Task 3: Building the convolutional network model.
a. You may choose the layers.
b. Print the summary and note the number of neurons and parameters of the model.
c. Compile the model and train it using the training data.
input = Input(shape = (28, 28, 1))
x = Conv2D(filters = 64, # total no of filters
kernel_size = 3, # size of the filters
activation = 'relu')(input)
x = MaxPooling2D()(x)
x = Conv2D(filters = 128,
kernel_size = 3,
activation = 'relu')(x)
x = MaxPooling2D()(x)
x = Conv2D(filters = 32,
kernel_size = 3,
activation = 'relu')(x)
x = MaxPooling2D()(x) # 3D matrix data
x = Flatten()(x) # Connecting to a Dense NN
output = Dense(10,activation = 'softmax')(x)
model = Model(inputs=input, outputs = output)
model.summary()
Model: "model"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_1 (InputLayer) [(None, 28, 28, 1)] 0
conv2d (Conv2D) (None, 26, 26, 64) 640
max_pooling2d (MaxPooling2 (None, 13, 13, 64) 0
D)
conv2d_1 (Conv2D) (None, 11, 11, 128) 73856
max_pooling2d_1 (MaxPoolin (None, 5, 5, 128) 0
g2D)
conv2d_2 (Conv2D) (None, 3, 3, 32) 36896
max_pooling2d_2 (MaxPoolin (None, 1, 1, 32) 0
g2D)
flatten (Flatten) (None, 32) 0
dense (Dense) (None, 10) 330
=================================================================
Total params: 111722 (436.41 KB)
Trainable params: 111722 (436.41 KB)
Non-trainable params: 0 (0.00 Byte)
_________________________________________________________________
model.compile(optimizer = 'adam',
loss= 'categorical_crossentropy',
metrics=['accuracy'])
history = model.fit(X_train, y_train, validation_data = (X_test, y_test), epochs =5)
Epoch 1/5
1875/1875 [==============================] - 137s 72ms/step - loss: 0.2087 - accuracy: 0.9360 - val_loss: 0.0903 - val_accuracy: 0.9724
Epoch 2/5
1875/1875 [==============================] - 130s 69ms/step - loss: 0.0745 - accuracy: 0.9767 - val_loss: 0.0543 - val_accuracy: 0.9845
Epoch 3/5
1875/1875 [==============================] - 128s 69ms/step - loss: 0.0518 - accuracy: 0.9839 - val_loss: 0.0585 - val_accuracy: 0.9830
Epoch 4/5
1875/1875 [==============================] - 132s 70ms/step - loss: 0.0387 - accuracy: 0.9879 - val_loss: 0.0608 - val_accuracy: 0.9830
Epoch 5/5
1875/1875 [==============================] - 128s 68ms/step - loss: 0.0310 - accuracy: 0.9901 - val_loss: 0.0418 - val_accuracy: 0.9864
score = model.evaluate(X_test, y_test)
print('Test Loss:', score[0])
print('Test accuracy:', score[1])
313/313 [==============================] - 6s 19ms/step - loss: 0.0418 - accuracy: 0.9864
Test Loss: 0.04178265482187271
Test accuracy: 0.9864000082015991
Task 4: Vary the number of layers and repeat step 3.
input = Input(shape = (28, 28, 1))
x = Conv2D(filters = 64,
kernel_size = 3,
activation = 'relu')(input)
x = AveragePooling2D()(x)
x = Conv2D(filters = 128,
kernel_size = 3,
activation = 'relu')(x)
x = AveragePooling2D()(x)
x = Conv2D(filters = 32,
kernel_size = 3,
activation = 'relu')(x)
x = AveragePooling2D()(x)
x = Flatten()(x)
output = Dense(10,activation = 'softmax')(x)
model1 = Model(inputs=input, outputs = output)
model1.summary()
Model: "model_1"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_2 (InputLayer) [(None, 28, 28, 1)] 0
conv2d_3 (Conv2D) (None, 26, 26, 64) 640
average_pooling2d (Average (None, 13, 13, 64) 0
Pooling2D)
conv2d_4 (Conv2D) (None, 11, 11, 128) 73856
average_pooling2d_1 (Avera (None, 5, 5, 128) 0
gePooling2D)
conv2d_5 (Conv2D) (None, 3, 3, 32) 36896
average_pooling2d_2 (Avera (None, 1, 1, 32) 0
gePooling2D)
flatten_1 (Flatten) (None, 32) 0
dense_1 (Dense) (None, 10) 330
=================================================================
Total params: 111722 (436.41 KB)
Trainable params: 111722 (436.41 KB)
Non-trainable params: 0 (0.00 Byte)
_________________________________________________________________
model1.compile(optimizer = 'adam',
loss= 'categorical_crossentropy',
metrics=['accuracy'])
history2 = model1.fit(X_train, y_train, validation_data = (X_test, y_test), epochs =5)
Epoch 1/5
1875/1875 [==============================] - 136s 72ms/step - loss: 0.2872 - accuracy: 0.9108 - val_loss: 0.1054 - val_accuracy: 0.9673
Epoch 2/5
1875/1875 [==============================] - 122s 65ms/step - loss: 0.1079 - accuracy: 0.9670 - val_loss: 0.0788 - val_accuracy: 0.9746
Epoch 3/5
1875/1875 [==============================] - 116s 62ms/step - loss: 0.0812 - accuracy: 0.9754 - val_loss: 0.0696 - val_accuracy: 0.9786
Epoch 4/5
1875/1875 [==============================] - 115s 61ms/step - loss: 0.0638 - accuracy: 0.9813 - val_loss: 0.0521 - val_accuracy: 0.9850
Epoch 5/5
1875/1875 [==============================] - 114s 61ms/step - loss: 0.0547 - accuracy: 0.9830 - val_loss: 0.0628 - val_accuracy: 0.9799
history_dict = history.history
accuracy_values = history_dict['accuracy']
val_accuracy_values = history_dict['val_accuracy']
epochs = range(1, len(accuracy_values) + 1)
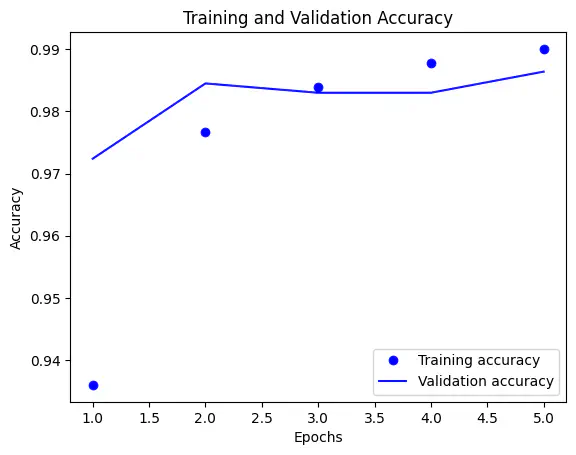
plt.plot(epochs, accuracy_values, 'bo', label='Training accuracy')
plt.plot(epochs, val_accuracy_values, 'b', label='Validation accuracy')
plt.title('Training and Validation Accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy') # Corrected label to 'Accuracy'
plt.legend()
plt.show()
score = model1.evaluate(X_test, y_test)
print('Test Loss:', score[0])
print('Test accuracy:', score[1])
313/313 [==============================] - 6s 18ms/step - loss: 0.0628 - accuracy: 0.9799
Test Loss: 0.06281796842813492
Test accuracy: 0.9799000024795532
Task 5: Implement the architecture of LeNet 5.
# LeNet architecture
inputs = Input(shape = (28, 28, 1))
x = Conv2D(filters = 6,
kernel_size = (5, 5),
activation = 'tanh', padding ='same', strides = 1)(inputs)
x = AveragePooling2D(strides=2,
pool_size =(2, 2))(x)
x = Conv2D(filters = 16,
kernel_size = (5, 5),
activation = 'tanh', padding='valid')(x)
x = AveragePooling2D(strides=2,
pool_size =(2, 2))(x)
x = Flatten()(x)
x = Dense(120, activation = 'tanh')(x)
x = Dense(84, activation='tanh')(x)
outputs = Dense(10, activation = 'softmax')(x)
lenet = Model(inputs=inputs, outputs = outputs)
lenet.summary()
Model: "model_2"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_3 (InputLayer) [(None, 28, 28, 1)] 0
conv2d_6 (Conv2D) (None, 28, 28, 6) 156
average_pooling2d_3 (Avera (None, 14, 14, 6) 0
gePooling2D)
conv2d_7 (Conv2D) (None, 10, 10, 16) 2416
average_pooling2d_4 (Avera (None, 5, 5, 16) 0
gePooling2D)
flatten_2 (Flatten) (None, 400) 0
dense_2 (Dense) (None, 120) 48120
dense_3 (Dense) (None, 84) 10164
dense_4 (Dense) (None, 10) 850
=================================================================
Total params: 61706 (241.04 KB)
Trainable params: 61706 (241.04 KB)
Non-trainable params: 0 (0.00 Byte)
_________________________________________________________________
lenet.compile(optimizer = 'adam',
loss= 'categorical_crossentropy',
metrics=['accuracy'])
history3 = lenet.fit(X_train, y_train, validation_data = (X_test, y_test), epochs =5)
Epoch 1/5
1875/1875 [==============================] - 43s 23ms/step - loss: 0.2280 - accuracy: 0.9322 - val_loss: 0.1025 - val_accuracy: 0.9681
Epoch 2/5
1875/1875 [==============================] - 42s 23ms/step - loss: 0.0836 - accuracy: 0.9740 - val_loss: 0.0680 - val_accuracy: 0.9771
Epoch 3/5
1875/1875 [==============================] - 47s 25ms/step - loss: 0.0583 - accuracy: 0.9820 - val_loss: 0.0651 - val_accuracy: 0.9783
Epoch 4/5
1875/1875 [==============================] - 43s 23ms/step - loss: 0.0442 - accuracy: 0.9862 - val_loss: 0.0525 - val_accuracy: 0.9840
Epoch 5/5
1875/1875 [==============================] - 42s 23ms/step - loss: 0.0365 - accuracy: 0.9878 - val_loss: 0.0564 - val_accuracy: 0.9834
score = lenet.evaluate(X_test, y_test)
print('Test Loss:', score[0])
print('Test accuracy:', score[1])
313/313 [==============================] - 3s 11ms/step - loss: 0.0564 - accuracy: 0.9834
Test Loss: 0.056421563029289246
Test accuracy: 0.9833999872207642
Task 6: Finally note which network gives you the best performance.
Model 1 gives us the highest Test accuracy of 98.5%
Learning Outcomes/Conclusion
Data Preprocessing: Understanding the essential data preprocessing steps, including one-hot encoding for class labels and feature normalization, to prepare data for deep learning.
CNN Model Construction: Building and training Convolutional Neural Networks (CNNs) with different layer configurations, gaining practical knowledge in network architecture design.
Layer Variation Impact: Discovering the effect of varying the number of layers in a CNN on model performance, which can help in making informed design choices.
LeNet-5 Implementation: Implementing the LeNet-5 architecture, a classic CNN design, to explore its structure and applications in image recognition tasks.
Performance Evaluation: Evaluating and comparing the performance of different network architectures on the MNIST dataset, with Model 1 identified as the best-performing model for the task.
Srihari Thyagarajan
B Tech AI Senior Student
Hi, I’m Haleshot, a final-year student studying B Tech Artificial Intelligence. I like projects relating to ML, AI, DL, CV, NLP, Image Processing, etc. Currently exploring Python, FastAPI, projects involving AI and platforms such as HuggingFace and Kaggle.