Discrete Fourier Transform
Experimenting with DFT, IDFT and matrices!
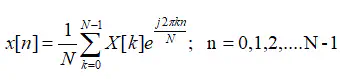 Formula used
Formula usedDiscrete Fourier Transform (DFT) in Python
Aim
The aim of this project is to obtain the twiddle factor matrix and perform the following tasks using it:
- Find the DFT and IDFT of the sequence [1, 2, 2, 1] using the twiddle factor matrix.
- Compute the DFT using matrix method and the FFT function.
- Observe and comment on the execution time required for each of the above methods.
Table of Contents
Software
This project is implemented using Python.
Prerequisite
To understand and work with this project, you should be familiar with the following concepts:
| Sr. No | Concepts |
|---|---|
| 1. | Discrete Fourier Transform |
Outcome
After successful completion of this experiment, students will be able to:
- Implement inverse and forward DFT on the given sequence.
- Can be found here.
Theory
Discrete Fourier Transform (DFT)
The Discrete Fourier Transform (DFT) is used for performing frequency analysis of discrete time signals. DFT provides a discrete frequency domain representation, whereas other transforms are continuous in the frequency domain.
The N-point DFT of a discrete time signal x[n] is given by the equation:
X(k) = Σ(x(n) * WNnk)
Where N is chosen such that N ≥ L (length of x[n]). The inverse DFT allows us to recover the sequence x[n] from the frequency samples.
The twiddle factor is given by:
WNnk = e(-jθ) = cos(θ) - j sin(θ)
Where θ = (2πnk) / N, n = 0 to N-1, and k = 0 to N-1.
Algorithm
The algorithm for performing the DFT using the twiddle factor matrix is as follows:
- Assign a value for the time period, N.
- Assign the frequency and sampling frequency.
- Give the sampling period rate, n.
- Define the sine function: sin(2π(f/fs)n).
- Find the DFT using the built-in function
fft(). - Find the DFT using the formula mentioned above.
- Plot the input function.
- Plot the DFT (absolute value) when the built-in function is used.
- Plot the DFT (absolute value) when the DFT formula is used.
- Display the output.
Formulae used to implement in user defined functions
DFT
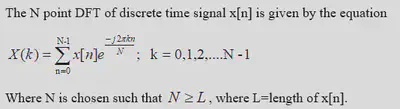
Inverse DFT
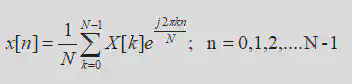
Obtaining Twiddle factor matrix for Forward DFT
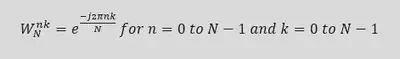
N = 4
l = np.zeros((4, 4), dtype = complex) # We get the values in cosθ - jsinθ due to which we need the array to be of complex datatypes.
for i in range(N):
for j in range(N):
real_part = int(math.cos(2 * math.pi * i * j/N))
img_part = int(math.sin(2 * math.pi * i * j/N)) * -1
l[i, j] = complex(real_part, img_part)
print(l)
[[ 1.+0.j 1.+0.j 1.+0.j 1.+0.j]
[ 1.+0.j 0.-1.j -1.+0.j 0.+1.j]
[ 1.+0.j -1.+0.j 1.+0.j -1.+0.j]
[ 1.+0.j 0.+1.j -1.+0.j 0.-1.j]]
Getting DFT for above DFT twiddle factor matrix
A = np.dot(l, np.transpose(x))
print(A)
[ 6.+0.j 0.+0.j -2.+0.j 0.+0.j]
Obtaining Twiddle factor matrix for Inverse DFT
N = 4
inv_l = np.zeros((4, 4), dtype = complex) # We get the values in cosθ - jsinθ due to which we need the array to be of complex datatypes.
for i in range(N):
for j in range(N):
real_part = int(math.cos(2 * math.pi * i * j/N))
img_part = int(math.sin(2 * math.pi * i * j/N))
inv_l[i, j] = complex(real_part, img_part)
print(inv_l)
[[ 1.+0.j 1.+0.j 1.+0.j 1.+0.j]
[ 1.+0.j 0.+1.j -1.+0.j 0.-1.j]
[ 1.+0.j -1.+0.j 1.+0.j -1.+0.j]
[ 1.+0.j 0.-1.j -1.+0.j 0.+1.j]]
Getting Invserse DFT for above Inverse DFT twiddle factor matrix
B = np.dot(inv_l, A)/N
print(B)
[1.+0.j 2.+0.j 1.+0.j 2.+0.j]
Comparing the above values of user defined algorithms to find DFT and FFT with the built in Transform functions of Numpy
P = np.fft.fft(x) # Obtaining the Forward Fourier Transform for the given sequence using numpy.fft.fft
Q = np.fft.ifft(x) # Obtaining the Inverse Fourier Transform for the given sequence using numpy.fft.ifft
print(P)
[ 6.+0.j 0.+0.j -2.+0.j 0.+0.j]
print(Q)
[ 1.5+0.j 0. +0.j -0.5+0.j 0. +0.j]
Conclusion:
- Obtaining the twiddle factor matrix .
- To find the DFT and IDFT of a given sequence using twiddle factor matrix.
- To compute the DFT and IDFT using matrix method/user defined and built in fft and ifft function.
- Implement Forward and inverse DFT on the given sequence.