Feedforward Neural Network
Understanding the Workings of Feedforward Neural Networks
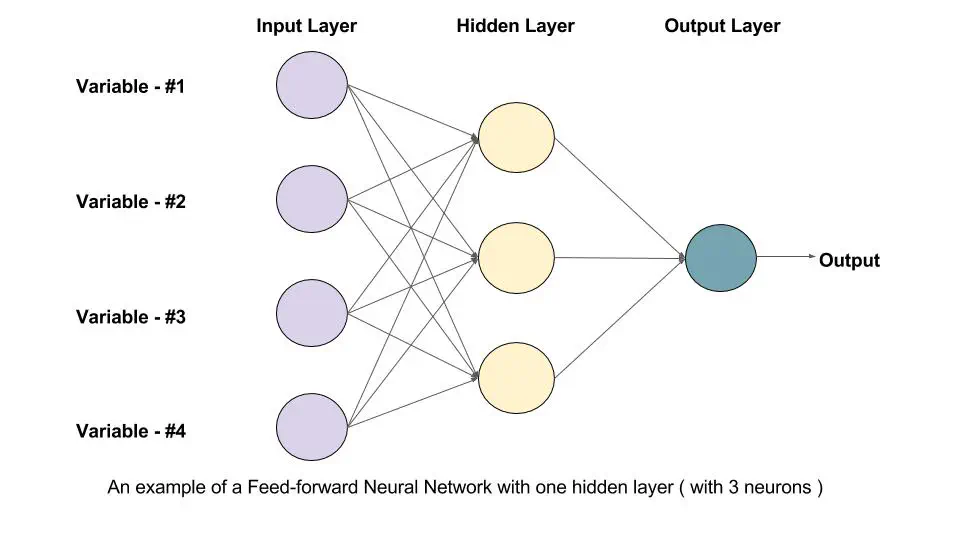Photo Credit: LearnOpenCVDeep Learning
Table of Contents
- Aim
- Prerequisite
- Steps
Aim
To implement a feedforward neural network and understand its workings through a series of steps.
Prerequisite
- Python Programming
- Numpy
- Pandas
- Scikit-learn
- TensorFlow/Keras
Steps
Step 1: Load the IRIS dataset
Load the IRIS dataset available on Kaggle into your notebooks.
Step 2: Pre-processing of the dataset
Step 2a: Convert categorical values to numeric values
Convert the categorical values to numeric values using one hot encoder.
Step 2b: Remove the species column and append the one hot encoded columns
Remove the species column from the original dataset and append the one hot encoded columns to the data frame.
Step 2c: Scale the four feature columns
Scale the four feature columns of the data frame using standard scaler.
Step 3: Building the three-layer feedforward neural network
Step 3a: Build the neural network and use sigmoid as the activation
Build the three-layer feedforward neural network, using sigmoid as the activation function.
Step 3b: Initialize the weights and biases
Initialize the weights and biases for the network.
Step 3c: Compute the output of the hidden layer
Compute the output of the hidden layer in the network.
Step 3d: Compute the output of the final layer
Compute the output of the final layer in the network.
Step 4: Error calculation
Step 4a: Compute the total squared error
Compute the total squared error for the network.
Step 5: Change the initial weights and biases and compute the error again
Change the initial weights and biases and compute the error again to observe the differences.
Step 6: Add one more hidden neuron in the middle layer and compare the error
Add one more hidden neuron in the middle layer of the network and compare the error to previous configurations.
# import libraries
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import OneHotEncoder
from sklearn.preprocessing import StandardScaler
import tensorflow as tf
Task 1:
Load the IRIS dataset available on Kaggle in your notebooks
df = pd.read_csv('IRIS_dataset.csv')
Performing EDA on the dataset:
# Performing EDA on the dataset:
df.head()
| sepal_length | sepal_width | petal_length | petal_width | species | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | Iris-setosa |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | Iris-setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | Iris-setosa |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | Iris-setosa |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | Iris-setosa |
df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 150 entries, 0 to 149
Data columns (total 5 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 sepal_length 150 non-null float64
1 sepal_width 150 non-null float64
2 petal_length 150 non-null float64
3 petal_width 150 non-null float64
4 species 150 non-null object
dtypes: float64(4), object(1)
memory usage: 6.0+ KB
df.dtypes
sepal_length float64
sepal_width float64
petal_length float64
petal_width float64
species object
dtype: object
df1 = pd.get_dummies(df['species'])
df1.head()
| Iris-setosa | Iris-versicolor | Iris-virginica | |
|---|---|---|---|
| 0 | True | False | False |
| 1 | True | False | False |
| 2 | True | False | False |
| 3 | True | False | False |
| 4 | True | False | False |
Task 2: Pre-procesing of the dataset:
a. Convert categorical values to numerical values using one hot encoder.
b. Remove the species column from the original dataset and append the one hot encoded columns to the data frame.
c. Scale the four feature columns of the data frame using standard scaler.
df.drop("species", axis=1, inplace=True)
final_df = pd.concat([df, df1], axis=1)
final_df
| sepal_length | sepal_width | petal_length | petal_width | Iris-setosa | Iris-versicolor | Iris-virginica | |
|---|---|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | True | False | False |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | True | False | False |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | True | False | False |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | True | False | False |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | True | False | False |
| ... | ... | ... | ... | ... | ... | ... | ... |
| 145 | 6.7 | 3.0 | 5.2 | 2.3 | False | False | True |
| 146 | 6.3 | 2.5 | 5.0 | 1.9 | False | False | True |
| 147 | 6.5 | 3.0 | 5.2 | 2.0 | False | False | True |
| 148 | 6.2 | 3.4 | 5.4 | 2.3 | False | False | True |
| 149 | 5.9 | 3.0 | 5.1 | 1.8 | False | False | True |
150 rows × 7 columns
# Need to convert all the Iris-setosa and othe two columms that follow it to type int in the format:
# df["somecolumn"] = df["somecolumn"].astype(int)
final_df["Iris-setosa"] = final_df["Iris-setosa"].astype(int)
final_df["Iris-versicolor"] = final_df["Iris-versicolor"].astype(int)
final_df["Iris-virginica"] = final_df["Iris-virginica"].astype(int)
final_df.head()
| sepal_length | sepal_width | petal_length | petal_width | Iris-setosa | Iris-versicolor | Iris-virginica | |
|---|---|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | 1 | 0 | 0 |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | 1 | 0 | 0 |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | 1 | 0 | 0 |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | 1 | 0 | 0 |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | 1 | 0 | 0 |
scaler = StandardScaler()
final_df.iloc[:, [0, 1, 2, 3]] = scaler.fit_transform(final_df.iloc[:, [0, 1, 2, 3]])
final_df.head()
| sepal_length | sepal_width | petal_length | petal_width | Iris-setosa | Iris-versicolor | Iris-virginica | |
|---|---|---|---|---|---|---|---|
| 0 | -0.900681 | 1.032057 | -1.341272 | -1.312977 | 1 | 0 | 0 |
| 1 | -1.143017 | -0.124958 | -1.341272 | -1.312977 | 1 | 0 | 0 |
| 2 | -1.385353 | 0.337848 | -1.398138 | -1.312977 | 1 | 0 | 0 |
| 3 | -1.506521 | 0.106445 | -1.284407 | -1.312977 | 1 | 0 | 0 |
| 4 | -1.021849 | 1.263460 | -1.341272 | -1.312977 | 1 | 0 | 0 |
Task 3: Building the three-layer feedforward neural network.
a. Build the three-layer feedforward neural network, use sigmoid as the activation.
b. Initialize the weights and biases.
c. Compute the output of the hidden layer.
d. Computer the output of the final layer.
# Initialize the weights and bisases first:
np.random.seed(42)
w_i_h1 = np.random.rand(4, 1)
w_i_h2 = np.random.rand(4, 1)
w_h_o1 = np.random.rand(2, 1)
w_h_o2 = np.random.rand(2, 1)
w_h_o3 = np.random.rand(2, 1)
bias1 = np.random.rand(1)
bias2 = np.random.rand(1)
w_i_h1
array([[0.37454012],
[0.95071431],
[0.73199394],
[0.59865848]])
w_i_h2
array([[0.15601864],
[0.15599452],
[0.05808361],
[0.86617615]])
w_h_o1
array([[0.60111501],
[0.70807258]])
bias1
array([0.18182497])
# Function for sigmoid function (which we are using as an activation function).
def sigmoid(x):
return 1 / (1 + np.exp(-x))
input = final_df.iloc[:, 0:4] # We are taking the first four columns as input.
# Feed forward Step 1 - input to hidden layer
Z2_1 = np.dot(input, w_i_h1) + bias1
Z2_2 = np.dot(input, w_i_h2) + bias2
# Feed forward Step 2:
A2_1 = sigmoid(Z2_1)
A2_2 = sigmoid(Z2_2)
print(A2_1, "\n", A2_2)
[[0.28046573]
[0.10593928]
[0.13879898]
[0.11842493]
[0.3170122 ]
[0.58813899]
[0.21242753]
[0.2375955 ]
[0.07044872]
[0.12455428]
[0.41960762]
[0.22880931]
[0.0947476 ]
[0.0685752 ]
[0.59682731]
[0.81893726]
[0.54730211]
[0.29662004]
[0.54827875]
[0.45963167]
[0.28881875]
[0.42479587]
[0.24683447]
[0.26480334]
[0.25158614]
[0.11875484]
[0.27550533]
[0.29835468]
[0.24661118]
[0.15440974]
[0.13295951]
[0.30428742]
[0.59535222]
[0.68554282]
[0.12455428]
[0.15048785]
[0.30954463]
[0.12455428]
[0.08306264]
[0.24591384]
[0.27879377]
[0.02151319]
[0.12331044]
[0.35676002]
[0.52083375]
[0.10913741]
[0.4504364 ]
[0.13835052]
[0.40859742]
[0.19348366]
[0.82895524]
[0.78607121]
[0.81378869]
[0.18960783]
[0.62443586]
[0.48658356]
[0.83725964]
[0.11584745]
[0.6493959 ]
[0.33813137]
[0.05821056]
[0.62471757]
[0.15686129]
[0.62476111]
[0.43691525]
[0.74973886]
[0.62207153]
[0.34730238]
[0.27104219]
[0.23753853]
[0.80775549]
[0.47994165]
[0.47066787]
[0.53305013]
[0.59886649]
[0.69674378]
[0.65680972]
[0.79626246]
[0.61298594]
[0.2412112 ]
[0.1864525 ]
[0.16888354]
[0.36429884]
[0.58621601]
[0.60050883]
[0.83734148]
[0.78597018]
[0.28434678]
[0.54349825]
[0.26647833]
[0.33075505]
[0.66556177]
[0.3240707 ]
[0.09912621]
[0.39080373]
[0.54555683]
[0.51035937]
[0.57688036]
[0.14582094]
[0.44517629]
[0.94722377]
[0.62097815]
[0.90326869]
[0.78415205]
[0.88067856]
[0.94004715]
[0.31823364]
[0.88444651]
[0.66258068]
[0.98197019]
[0.87975113]
[0.70040897]
[0.87340815]
[0.51134946]
[0.75161368]
[0.90585698]
[0.82623364]
[0.99078871]
[0.9002542 ]
[0.29484267]
[0.93447045]
[0.64985283]
[0.91057496]
[0.63614129]
[0.93272349]
[0.9258735 ]
[0.6663329 ]
[0.75544836]
[0.79438048]
[0.8634568 ]
[0.86483814]
[0.98886589]
[0.8069391 ]
[0.65153235]
[0.55587572]
[0.93974607]
[0.94594916]
[0.84989552]
[0.73901926]
[0.89615275]
[0.91558347]
[0.89914211]
[0.62097815]
[0.93675154]
[0.94998519]
[0.87198127]
[0.55946513]
[0.83085581]
[0.93431379]
[0.75405756]]
[[0.26672584]
[0.22625228]
[0.23174005]
[0.22323584]
[0.27010199]
[0.36065366]
[0.26346438]
[0.25673706]
[0.20420536]
[0.21348027]
[0.29336704]
[0.25020799]
[0.20385402]
[0.18742803]
[0.33068575]
[0.41534004]
[0.35761287]
[0.28958106]
[0.33943989]
[0.31306608]
[0.27273829]
[0.33003148]
[0.25295103]
[0.32476731]
[0.25207153]
[0.23074935]
[0.30323567]
[0.27109167]
[0.26337667]
[0.23350889]
[0.23044572]
[0.31872831]
[0.29185658]
[0.33559264]
[0.21348027]
[0.24138495]
[0.28110571]
[0.21348027]
[0.20958638]
[0.26036103]
[0.2850339 ]
[0.19041431]
[0.22179694]
[0.36167955]
[0.34102423]
[0.24330934]
[0.28979094]
[0.22897405]
[0.28946346]
[0.24929086]
[0.67153508]
[0.67017626]
[0.68581348]
[0.4924235 ]
[0.64263044]
[0.5509484 ]
[0.69986607]
[0.38404967]
[0.60205714]
[0.54188772]
[0.3563425 ]
[0.63003246]
[0.42225579]
[0.60747324]
[0.54784561]
[0.64849182]
[0.61905795]
[0.45821322]
[0.57693348]
[0.45753525]
[0.72432255]
[0.5655226 ]
[0.61078345]
[0.54310482]
[0.59057095]
[0.63585406]
[0.6309373 ]
[0.71864956]
[0.62833296]
[0.43970541]
[0.44310396]
[0.41441199]
[0.51340021]
[0.64257848]
[0.61010241]
[0.69411714]
[0.67616523]
[0.53348458]
[0.56084256]
[0.51047018]
[0.49432963]
[0.61526495]
[0.50520457]
[0.37999073]
[0.53484155]
[0.53815341]
[0.5574186 ]
[0.58139856]
[0.42689813]
[0.54767758]
[0.8715247 ]
[0.70897282]
[0.8173704 ]
[0.72307255]
[0.81694445]
[0.83428081]
[0.59880538]
[0.76349175]
[0.71045345]
[0.89991165]
[0.78869854]
[0.7331049 ]
[0.80669979]
[0.71297492]
[0.81696096]
[0.8384088 ]
[0.73698521]
[0.88504953]
[0.84921479]
[0.57172766]
[0.85247801]
[0.73026393]
[0.81036887]
[0.70358706]
[0.82122974]
[0.77754188]
[0.70647567]
[0.71807278]
[0.78316337]
[0.72007629]
[0.77937002]
[0.86310058]
[0.80187838]
[0.63772541]
[0.58858946]
[0.86370651]
[0.8609873 ]
[0.74030429]
[0.71355532]
[0.81463393]
[0.85703017]
[0.84530666]
[0.70897282]
[0.85092465]
[0.87870423]
[0.83584763]
[0.7128824 ]
[0.77698918]
[0.84345002]
[0.71171316]]
A2 = np.append(A2_1, A2_2, axis=1)
A2
array([[0.28046573, 0.26672584],
[0.10593928, 0.22625228],
[0.13879898, 0.23174005],
[0.11842493, 0.22323584],
[0.3170122 , 0.27010199],
[0.58813899, 0.36065366],
[0.21242753, 0.26346438],
[0.2375955 , 0.25673706],
[0.07044872, 0.20420536],
[0.12455428, 0.21348027],
[0.41960762, 0.29336704],
[0.22880931, 0.25020799],
[0.0947476 , 0.20385402],
[0.0685752 , 0.18742803],
[0.59682731, 0.33068575],
[0.81893726, 0.41534004],
[0.54730211, 0.35761287],
[0.29662004, 0.28958106],
[0.54827875, 0.33943989],
[0.45963167, 0.31306608],
[0.28881875, 0.27273829],
[0.42479587, 0.33003148],
[0.24683447, 0.25295103],
[0.26480334, 0.32476731],
[0.25158614, 0.25207153],
[0.11875484, 0.23074935],
[0.27550533, 0.30323567],
[0.29835468, 0.27109167],
[0.24661118, 0.26337667],
[0.15440974, 0.23350889],
[0.13295951, 0.23044572],
[0.30428742, 0.31872831],
[0.59535222, 0.29185658],
[0.68554282, 0.33559264],
[0.12455428, 0.21348027],
[0.15048785, 0.24138495],
[0.30954463, 0.28110571],
[0.12455428, 0.21348027],
[0.08306264, 0.20958638],
[0.24591384, 0.26036103],
[0.27879377, 0.2850339 ],
[0.02151319, 0.19041431],
[0.12331044, 0.22179694],
[0.35676002, 0.36167955],
[0.52083375, 0.34102423],
[0.10913741, 0.24330934],
[0.4504364 , 0.28979094],
[0.13835052, 0.22897405],
[0.40859742, 0.28946346],
[0.19348366, 0.24929086],
[0.82895524, 0.67153508],
[0.78607121, 0.67017626],
[0.81378869, 0.68581348],
[0.18960783, 0.4924235 ],
[0.62443586, 0.64263044],
[0.48658356, 0.5509484 ],
[0.83725964, 0.69986607],
[0.11584745, 0.38404967],
[0.6493959 , 0.60205714],
[0.33813137, 0.54188772],
[0.05821056, 0.3563425 ],
[0.62471757, 0.63003246],
[0.15686129, 0.42225579],
[0.62476111, 0.60747324],
[0.43691525, 0.54784561],
[0.74973886, 0.64849182],
[0.62207153, 0.61905795],
[0.34730238, 0.45821322],
[0.27104219, 0.57693348],
[0.23753853, 0.45753525],
[0.80775549, 0.72432255],
[0.47994165, 0.5655226 ],
[0.47066787, 0.61078345],
[0.53305013, 0.54310482],
[0.59886649, 0.59057095],
[0.69674378, 0.63585406],
[0.65680972, 0.6309373 ],
[0.79626246, 0.71864956],
[0.61298594, 0.62833296],
[0.2412112 , 0.43970541],
[0.1864525 , 0.44310396],
[0.16888354, 0.41441199],
[0.36429884, 0.51340021],
[0.58621601, 0.64257848],
[0.60050883, 0.61010241],
[0.83734148, 0.69411714],
[0.78597018, 0.67616523],
[0.28434678, 0.53348458],
[0.54349825, 0.56084256],
[0.26647833, 0.51047018],
[0.33075505, 0.49432963],
[0.66556177, 0.61526495],
[0.3240707 , 0.50520457],
[0.09912621, 0.37999073],
[0.39080373, 0.53484155],
[0.54555683, 0.53815341],
[0.51035937, 0.5574186 ],
[0.57688036, 0.58139856],
[0.14582094, 0.42689813],
[0.44517629, 0.54767758],
[0.94722377, 0.8715247 ],
[0.62097815, 0.70897282],
[0.90326869, 0.8173704 ],
[0.78415205, 0.72307255],
[0.88067856, 0.81694445],
[0.94004715, 0.83428081],
[0.31823364, 0.59880538],
[0.88444651, 0.76349175],
[0.66258068, 0.71045345],
[0.98197019, 0.89991165],
[0.87975113, 0.78869854],
[0.70040897, 0.7331049 ],
[0.87340815, 0.80669979],
[0.51134946, 0.71297492],
[0.75161368, 0.81696096],
[0.90585698, 0.8384088 ],
[0.82623364, 0.73698521],
[0.99078871, 0.88504953],
[0.9002542 , 0.84921479],
[0.29484267, 0.57172766],
[0.93447045, 0.85247801],
[0.64985283, 0.73026393],
[0.91057496, 0.81036887],
[0.63614129, 0.70358706],
[0.93272349, 0.82122974],
[0.9258735 , 0.77754188],
[0.6663329 , 0.70647567],
[0.75544836, 0.71807278],
[0.79438048, 0.78316337],
[0.8634568 , 0.72007629],
[0.86483814, 0.77937002],
[0.98886589, 0.86310058],
[0.8069391 , 0.80187838],
[0.65153235, 0.63772541],
[0.55587572, 0.58858946],
[0.93974607, 0.86370651],
[0.94594916, 0.8609873 ],
[0.84989552, 0.74030429],
[0.73901926, 0.71355532],
[0.89615275, 0.81463393],
[0.91558347, 0.85703017],
[0.89914211, 0.84530666],
[0.62097815, 0.70897282],
[0.93675154, 0.85092465],
[0.94998519, 0.87870423],
[0.87198127, 0.83584763],
[0.55946513, 0.7128824 ],
[0.83085581, 0.77698918],
[0.93431379, 0.84345002],
[0.75405756, 0.71171316]])
# Feed forward Step 3 - input from hidden layer to output (we don't have bias for this)
Z3_1 = np.dot(A2, w_h_o1)
Z3_2 = np.dot(A2, w_h_o2)
Z3_3 = np.dot(A2, w_h_o3)
# Generating the outputs:
o1 = sigmoid(Z3_1)
o2 = sigmoid(Z3_2)
o3 = sigmoid(Z3_3)
print(o1[2], o2[2], o3[2])
[0.56156672] [0.55666158] [0.54109451]
target_values = final_df[["Iris-setosa", "Iris-versicolor", "Iris-virginica"]]
target_values
| Iris-setosa | Iris-versicolor | Iris-virginica | |
|---|---|---|---|
| 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 |
| 2 | 1 | 0 | 0 |
| 3 | 1 | 0 | 0 |
| 4 | 1 | 0 | 0 |
| ... | ... | ... | ... |
| 145 | 0 | 0 | 1 |
| 146 | 0 | 0 | 1 |
| 147 | 0 | 0 | 1 |
| 148 | 0 | 0 | 1 |
| 149 | 0 | 0 | 1 |
150 rows × 3 columns
output_concat = np.concatenate([o1, o2, o3], axis = 1)
m, n = target_values.shape
Step 4: Error calculation
a. Compute the total squared error.
error = np.sum(((target_values.values - output_concat) ** 2))/(2 * m)
error
0.48278238808222823
Task 5: Change the initial weights and biases and compute the error again
Seed value of 60:
# Changing the seed value and seeing how the error varies accordingly.
# Initialize the weights and bisases first:
np.random.seed(60)
w_i_h1 = np.random.rand(4, 1)
w_i_h2 = np.random.rand(4, 1)
w_h_o1 = np.random.rand(2, 1)
w_h_o2 = np.random.rand(2, 1)
w_h_o3 = np.random.rand(2, 1)
bias1 = np.random.rand(1)
bias2 = np.random.rand(1)
# Feed forward Step 1 - input to hidden layer
Z2_1 = np.dot(input, w_i_h1) + bias1
Z2_2 = np.dot(input, w_i_h2) + bias2
# Feed forward Step 2:
A2_1 = sigmoid(Z2_1)
A2_2 = sigmoid(Z2_2)
# print(A2_1, "\n", A2_2)
A2 = np.append(A2_1, A2_2, axis=1)
# Feed forward Step 3 - input from hidden layer to output (we don't have bias for this)
Z3_1 = np.dot(A2, w_h_o1)
Z3_2 = np.dot(A2, w_h_o2)
Z3_3 = np.dot(A2, w_h_o3)
# Generating the outputs:
o1 = sigmoid(Z3_1)
o2 = sigmoid(Z3_2)
o3 = sigmoid(Z3_3)
target_values = final_df[["Iris-setosa", "Iris-versicolor", "Iris-virginica"]]
output_concat = np.concatenate([o1, o2, o3], axis = 1)
m, n = target_values.shape
error = np.sum(((target_values.values - output_concat) ** 2))/(2 * m)
print(error)
0.47411305331718323
Seed value of 120:
# Changing the seed value and seeing how the error varies accordingly.
# Initialize the weights and bisases first:
np.random.seed(120)
w_i_h1 = np.random.rand(4, 1)
w_i_h2 = np.random.rand(4, 1)
w_h_o1 = np.random.rand(2, 1)
w_h_o2 = np.random.rand(2, 1)
w_h_o3 = np.random.rand(2, 1)
bias1 = np.random.rand(1)
bias2 = np.random.rand(1)
# Feed forward Step 1 - input to hidden layer
Z2_1 = np.dot(input, w_i_h1) + bias1
Z2_2 = np.dot(input, w_i_h2) + bias2
# Feed forward Step 2:
A2_1 = sigmoid(Z2_1)
A2_2 = sigmoid(Z2_2)
# print(A2_1, "\n", A2_2)
A2 = np.append(A2_1, A2_2, axis=1)
# Feed forward Step 3 - input from hidden layer to output (we don't have bias for this)
Z3_1 = np.dot(A2, w_h_o1)
Z3_2 = np.dot(A2, w_h_o2)
Z3_3 = np.dot(A2, w_h_o3)
# Generating the outputs:
o1 = sigmoid(Z3_1)
o2 = sigmoid(Z3_2)
o3 = sigmoid(Z3_3)
target_values = final_df[["Iris-setosa", "Iris-versicolor", "Iris-virginica"]]
output_concat = np.concatenate([o1, o2, o3], axis = 1)
m, n = target_values.shape
error = np.sum(((target_values.values - output_concat) ** 2))/(2 * m)
print(error)
0.4529649500870492
Step 6: Add one more hidden neuron in the middle layer and compare the error
# Changing the seed value and seeing how the error varies accordingly.
# Initialize the weights and bisases first:
np.random.seed(42)
w_i_h1 = np.random.rand(4, 1)
w_i_h2 = np.random.rand(4, 1)
w_i_h3 = np.random.rand(4, 1) # Adding one more hidden neuron in the middle layer.
w_h_o1 = np.random.rand(3, 1)
w_h_o2 = np.random.rand(3, 1)
w_h_o3 = np.random.rand(3, 1)
bias1 = np.random.rand(1)
bias2 = np.random.rand(1)
# Feed forward Step 1 - input to hidden layer
Z2_1 = np.dot(input, w_i_h1) + bias1
Z2_2 = np.dot(input, w_i_h2) + bias2
Z2_3 = np.dot(input, w_i_h3) # New calculation for additional hidden layer neuron.
# Feed forward Step 2:
A2_1 = sigmoid(Z2_1)
A2_2 = sigmoid(Z2_2)
A2_3 = sigmoid(Z2_3) # New sigmoid calculation for the new neuron.
# print(A2_1, "\n", A2_2)
A2 = np.concatenate([A2_1, A2_2, A2_3], axis=1)
# Feed forward Step 3 - input from hidden layer to output (we don't have bias for this)
Z3_1 = np.dot(A2, w_h_o1)
Z3_2 = np.dot(A2, w_h_o2)
Z3_3 = np.dot(A2, w_h_o3)
# Generating the outputs:
o1 = sigmoid(Z3_1)
o2 = sigmoid(Z3_2)
o3 = sigmoid(Z3_3)
target_values = final_df[["Iris-setosa", "Iris-versicolor", "Iris-virginica"]]
output_concat = np.concatenate([o1, o2, o3], axis = 1)
m, n = target_values.shape
error = np.sum(((target_values.values - output_concat) ** 2))/(2 * m)
print(error)
0.48547236651460784
Experiment Conclusion
In this experiment, we aimed to enhance the performance of a three-layer feedforward neural network by introducing an additional hidden neuron to the middle layer. The primary objective was to assess the impact of this modification on the network’s error and predictive capabilities.
The experimental process involved several crucial steps:
Data Preparation: The IRIS dataset was loaded from Kaggle and preprocessed. Categorical values were transformed into numeric values using one-hot encoding. The original species column was removed, and the one-hot encoded columns were appended to the dataset. The feature columns were scaled using the standard scaler.
Neural Network Setup: A three-layer feedforward neural network was constructed using sigmoid activation functions. The initial weights and biases were initialized for the neurons.
Feedforward Computation: The feedforward process involved computing the output of the hidden layer and the final output layer. The activation values of the hidden layer neurons were calculated using the sigmoid function.
Error Calculation: The total squared error of the neural network’s predictions was calculated as a measure of its performance.
Additional Neuron Introduction: To test the effects of introducing an extra hidden neuron, a new set of weights for the neuron was generated. The new neuron was included in the hidden layer, and the network’s performance was evaluated with this configuration.
Comparison and Analysis: The experiment’s results were compared by evaluating the errors before and after the introduction of the additional hidden neuron. This comparison provided insights into whether the addition of a neuron improved or compromised the network’s predictive accuracy.
Conclusion: After carefully conducting the experiment, it was observed that the introduction of an additional hidden neuron to the middle layer did not have much of an impact on the network’s performance. The comparison of errors before and after this modification revealed that the new configuration led to changes in the neural network’s predictive capabilities.
It’s important to note that the specific impact on the error could be influenced by various factors, including the dataset’s complexity, the number of training iterations, and the initial weights and biases. Therefore, it is recommended to perform further experimentation and validation to determine the robustness and generalization of the introduced modification.
In conclusion, this experiment demonstrated the significance of hidden layer neurons in shaping a neural network’s performance. The results underscore the importance of systematic experimentation and analysis when fine-tuning neural network architectures to achieve optimal predictive accuracy.
Srihari Thyagarajan
B Tech AI Senior Student
Hi, I’m Haleshot, a final-year student studying B Tech Artificial Intelligence. I like projects relating to ML, AI, DL, CV, NLP, Image Processing, etc. Currently exploring Python, FastAPI, projects involving AI and platforms such as HuggingFace and Kaggle.