Round Robin
Implementing the Round Robin Process Scheduling Algorithm
 Program output
Program outputRound Robin Scheduling Algorithm
The Round Robin (RR) scheduling algorithm is one of the oldest, simplest, fairest, and most widely used algorithms in operating systems. It dispatches processes in a First-In-First-Out (FIFO) manner but assigns them a limited amount of CPU time known as a time-slice or a quantum. If a process does not complete within its time-slice, the CPU is preempted and given to the next process waiting in the queue. The preempted process is then placed at the back of the ready list. Round Robin Scheduling is preemptive, making it effective in time-sharing environments where the system needs to guarantee reasonable response times for interactive users.
Table of Contents
- Introduction
- Characteristics of Round-Robin Scheduling
- Calculating Average Waiting Time
- Example Processes
- Output
Introduction
The Round Robin scheduling algorithm provides fairness by allocating CPU time to processes in a cyclic manner. Each process is executed for a fixed time quantum, and if the process doesn’t complete within the quantum, it is preempted and added back to the ready queue. This algorithm is widely implemented in most operating systems and is suitable for time-sharing environments.
Characteristics of Round-Robin Scheduling
Here are the important characteristics of Round-Robin Scheduling:
- Round Robin is a preemptive algorithm.
- The CPU is shifted to the next process after a fixed interval of time called a time quantum or time slice.
- The preempted process is added to the end of the queue.
- Round Robin is a hybrid model that is clock-driven.
- The time slice should be a minimum assigned time for a specific task, but it may vary across different operating systems.
- It is a real-time algorithm that responds to events within a specific time limit.
- Round Robin is one of the oldest, fairest, and easiest scheduling algorithms.
- It is a widely used scheduling method in traditional operating systems.
Calculating Average Waiting Time
Average waiting time (AWT) is a crucial parameter to evaluate the performance of any scheduling algorithm. AWT represents the average waiting time of processes in the queue, waiting for the scheduler to select them for execution.
Example Processes
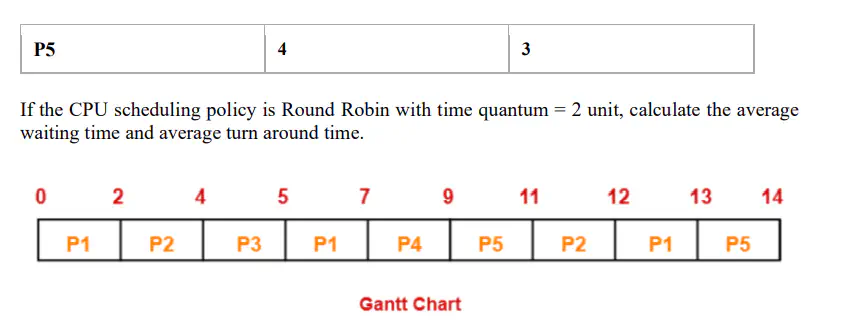
Consider the following set of 5 processes whose arrival time and burst time are given:


Output
The output of the .py file implementing the Round Robin scheduling algorithm is shown below:



Please refer to the Round Robin Repository for the complete code implementation.
For more information on scheduling algorithms and their analysis, please check the related files and code in this repository.
# Round Robin Algorithm with and without Arrival Time (Preemptive)
# To Find - Turn Around Time and Wait Time and their respective average times
# Functions to sort the list which contains Arrival and Burst Times according to Burst Time
# import libraries
from re import S
from tabulate import tabulate # For printing the result in a Tabular Format
def sorting_burst(l):
return l[2] # Returns the Third element of the list which is Burst Time
def sorting_arrival(l):
return l[1] # Returns the Second element of the list which is Arrival Time
def Turn_Around_Time(P, limit):
# Declaring Variables for Calculating Total Turn Around Time
total_tat = 0
for i in range(limit):
tat = P[i][5] - P[i][1]
total_tat += tat # Formula For Turn Around Time -> Completion Time - Arrival TIme
P[i].append(tat) # Appending the Turn Around Time to the List
avg_tat = total_tat/limit
return avg_tat
def Waiting_Time(P, limit):
# Declaring Variables for Calculating Total Waiting Time
total_wt = 0
for i in range(limit):
wt = P[i][6] - P[i][4]
total_wt += wt # Formula For Waiting Time -> Turn Around Time - Burst Time
P[i].append(wt) # Appending the Waiting Time to the List
avg_wt = total_wt/limit
return avg_wt
def Logic(P, limit, tq):
completed_processes = []
arrived = [] # Contains Processes which have completed their respective execution
exit_time = [] # To note the completion time of a process -> the end time of previous process + burst time of current process
completion_time = 0 # Execution Time for a process
# Sorting Processes by Arrival Time
P.sort(key=sorting_arrival)
while True: # The loop runs till all the processes have been executed successfully
not_arrived = [] # Contains Processes which have not completed their respective execution
buffer = []
for i in range(limit):
if(P[i][1] <= completion_time and P[i][3] == 0):# Checking whether the arrival time of the process is less
# than Completion time or not and if the process has not been executed
a = 0
if(len(arrived) != 0):
for j in range(len(arrived)):
if (P[i][0] == arrived[j][0]):
a = 1
if a == 0: # Adding a process once it's completed, to the Arrived list
buffer.extend([P[i][0], P[i][1], P[i][2], P[i][4]]) # Appending Process ID, AT, BT and Burst Time which
# will be used as Remaineder Time - Time Quantum - Burst Time
arrived.append(buffer)
buffer = []
if (len(arrived) != 0 and len(completed_processes) != 0): # Inserting a recently executed process at the
# end of the arrived list
for j in range(len(arrived)):
if(arrived[j][0] == completed_processes[len(completed_processes) - 1]):
arrived.insert((len(arrived) - 1), arrived.pop(j))
elif P[i][3] == 0:
buffer.extend([P[i][0], P[i][1], P[i][2], P[i][4]]) # Appending Process ID, AT, BT and Burst Time which
# will be used as Remaineder Time - Time Quantum - Burst Time
not_arrived.append(buffer)
buffer = []
if len(arrived) == 0 and len(not_arrived) == 0:
break
if(len(arrived) != 0):
if arrived[0][2] > tq: # Process has Greater Burst TIme than Time Quantum
completion_time += tq
exit_time.append(completion_time)
completed_processes.append(arrived[0][0])
for j in range(limit):
if(P[j][0] == arrived[0][0]):
break
P[j][2] -= tq # Reducing Time Quantum from Burst time
arrived.pop(0) # Popping the completed process
elif (arrived[0][2] <= tq): # If the Burst Time is Less than or Equal to Time Quantum
completion_time += arrived[0][2]
exit_time.append(completion_time)
completed_processes.append(arrived[0][0])
for j in range(limit):
if(P[j][0] == arrived[0][0]):
break
P[j][2] = 0 # Setting the Burst Time as 0 since Process gets executed completely
P[j][3] = 1 # Setting Completion status as 1 -> implies process has been executed successfully.
P[j].append(completion_time)
arrived.pop(0) # Popping the completed process
elif (len(arrived) == 0):
if completion_time < not_arrived[0][1]: # Checking completion time with arrival time of process
# which hasn't been executed
completion_time = not_arrived[0][1]
if not_arrived[0][2] > tq: # Process has Greater Burst Time than Time Quantum
completion_time += tq
exit_time.append(completion_time)
completed_processes.append(not_arrived[0][0])
for j in range(limit):
if(P[j][0] == not_arrived[0][0]):
break
P[j][2] -= tq # Reducing Time Quantum from Burst time
elif (not_arrived[0][2] <= tq): # If the Burst Time is Less than or Equal to Time Quantum
completion_time += not_arrived[0][2]
exit_time.append(completion_time)
completed_processes.append(not_arrived[0][0])
for j in range(limit):
if(P[j][0] == not_arrived[0][0]):
break
P[j][2] = 0 # Setting the Burst Time as 0 since Process gets executed completely
P[j][3] = 1 # Setting Completion status as 1 -> implies process has been executed successfully.
P[j].append(completion_time)
tat = Turn_Around_Time(P, limit)
wt = Waiting_Time(P, limit)
P.sort(key=sorting_burst) # Sorting the List by Burst Time (Order in which processes are executed)
headers = ["Process Number", "Arrival Time", "Remainder Burst Time", "Completed Status", "Original Burst Time", "Total Execution Time", "Turn Around Time", "Waiting Time"]
print(tabulate(P, headers, tablefmt="psql"))
# Printing the Average Waiting and Turn Around Time
print("\nAverage Waiting Time is = ", round(wt, 2)) # Rounding off Average Waiting Time to 2 Decimal places
print("Average Turn Around Time is = ", round(tat, 2)) # Rounding off Average Turn Around Time to 2 Decimal places
def main():
run = True
while(run):
# Declaring arrays
processes = []
print("\nMenu\nDo you want to assume : \n1. Arrival Time as 0\n2. Input Arrival Time\n3. Exit\n")
ch = int(input("Enter Your Choice : "))
if ch == 1:
limit_process = int(input("Enter the Number of Processes : "))
for i in range(limit_process):
p = []
arrival = 0
burst = int(input("Enter the Burst Time for process {} : ".format(i)))
process_id = "P" + str(i + 1)
p.extend([process_id, arrival, burst, 0, burst]) # Forming a list of info entered by the user, 0 is for completion status
processes.append(p)
time_quantum = int(input("Enter the Time Quantum : ")) # Inputting Time Quantum from user
Logic(processes , limit_process, time_quantum)
run = int(input("\nWant to continue? (Yes = Input 1/false = Input 0) : "))
elif ch == 2:
limit_process = int(input("Enter the Number of Processes : "))
for i in range(limit_process):
p = []
arrival = int(input("Enter the Arrival Time for process {} : ".format(i)))
burst = int(input("Enter the Burst Time for process {} : ".format(i)))
process_id = "P" + str(i + 1)
p.extend([process_id, arrival, burst, 0, burst])
processes.append(p)
time_quantum = int(input("Enter the Time Quantum : ")) # Inputting Time Quantum from user
Logic(processes, limit_process, time_quantum)
run = int(input("\nWant to continue? (Yes = Input 1/false = Input 0) : "))
elif ch == 3:
print("Thank You!")
exit(0)
else:
print("Invalid Choice!")
run = int(input("\nWant to continue? (Yes = Input 1/false = Input 0) : "))
main()
Menu
Do you want to assume :
1. Arrival Time as 0
2. Input Arrival Time
3. Exit
Enter Your Choice : 2
Enter the Number of Processes : 5
Enter the Arrival Time for process 0 : 0
Enter the Burst Time for process 0 : 5
Enter the Arrival Time for process 1 : 1
Enter the Burst Time for process 1 : 3
Enter the Arrival Time for process 2 : 2
Enter the Burst Time for process 2 : 1
Enter the Arrival Time for process 3 : 3
Enter the Burst Time for process 3 : 2
Enter the Arrival Time for process 4 : 4
Enter the Burst Time for process 4 : 3
Enter the Time Quantum : 2
+------------------+----------------+------------------------+--------------------+-----------------------+------------------------+--------------------+----------------+
| Process Number | Arrival Time | Remainder Burst Time | Completed Status | Original Burst Time | Total Execution Time | Turn Around Time | Waiting Time |
|------------------+----------------+------------------------+--------------------+-----------------------+------------------------+--------------------+----------------|
| P1 | 0 | 0 | 1 | 5 | 13 | 13 | 8 |
| P2 | 1 | 0 | 1 | 3 | 12 | 11 | 8 |
| P3 | 2 | 0 | 1 | 1 | 5 | 3 | 2 |
| P4 | 3 | 0 | 1 | 2 | 9 | 6 | 4 |
| P5 | 4 | 0 | 1 | 3 | 14 | 10 | 7 |
+------------------+----------------+------------------------+--------------------+-----------------------+------------------------+--------------------+----------------+
Average Waiting Time is = 5.8
Average Turn Around Time is = 8.6
Want to continue? (Yes = Input 1/false = Input 0) : 0